디지털 회로 설계에서 부울 함수(Boolean Function)는 시스템의 논리적 동작을 정의하는 데 있어 필수적인 요소이다. 그러나 복잡한 논리식을 그대로 회로로 구현하면 게이트 수 증가, 소비 전력 상승, 전파 지연 확대 등의 문제를 야기할 수 있다. 이러한 문제를 해결하기 위해 부울 함수를 간략화하는 다양한 기법이 존재하며, 이 글에서는 대표적인 간략화 기법과 그 활용 방법에 대해 살펴보고자 한다.
1. 부울 대수의 법칙에 의한 간략화
1.1 부울 함수를 간략화하는 이유
부울 함수를 간략화하는 주된 목적은 다음과 같다.
- 논리 회로 구현 시 게이트 수를 줄일 수 있다.
- 회로의 소비 전력을 줄일 수 있다.
- 논리 신호의 전파 지연(Propagation Delay)을 줄일 수 있다.
- 전체 회로의 안정성과 속도를 개선할 수 있다.
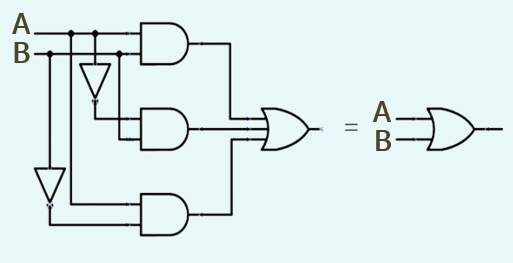
1.2 간략화 방법의 종류
부울 함수 간략화에는 여러 가지 방법이 존재하며, 주로 다음 네 가지 방식이 사용된다.
- 부울 대수의 공리 및 법칙을 이용하는 방법
- 카르노 맵(Karnaugh Map)을 이용하는 방법 (주로 4변수 이하의 함수에 효과적)
- 표 기반(Table Method) 방법 (5변수 이상에서는 컴퓨터 프로그램 활용)
- 퀸-맥클러스키(QM: Quine–McCluskey) 알고리즘 (컴퓨터 기반의 체계적인 간소화)
1.3 부울 대수를 이용한 간략화 방법
(1) 항 결합법 (Combining Terms)
- 각 항에서 공통된 변수를 찾아 이를 묶어줌으로써 간략화함.
예: AB + AB' = A

(2) 항 제거법 (Elimination Method)
- 흡수법칙(A + AB = A)과 배분법칙을 역으로 사용하여 불필요한 항을 제거함.
예: A(B + B') = A(1) = A

(3) 간략화 예
- 원래 식: A'B + A'BC + A'B'C
- 간략화 후: A'B + A'B'C → A'B + A'B'C = A'B



이러한 방식은 변수 수가 적고 간단한 경우에 유효하다. 복잡한 논리식의 경우 다음 장에서 설명할 카르노 맵(Karnaugh Map) 방식이 더 효과적이다.
2. 카르노 맵(Karnaugh Map, K-Map)에 의한 간략화
2.1 카르노 맵의 개요
카르노 맵은 시각적인 방법으로 부울 함수를 간략화하는 도구이며, 불 대수(Boolean Algebra)의 확장 표현을 사람이 직관적으로 인식 가능한 형태로 변환하여, 변수 간의 관계를 시각적으로 묶어 간소화하는 방법이다.
- 각 셀(Cell)은 하나의 최소항(minterm)을 나타낸다.
- 맵의 행과 열은 변수들의 그레이 코드(Gray Code) 순서로 배열된다.
- 이웃한 셀들끼리 묶음(Grouping)을 통해 공통된 변수를 찾아 간단한 논리식으로 표현할 수 있다.



2.2 무관항(Don't Care, d)
무관항은 특정 입력 조합에서 출력이 사용되지 않거나 결과에 영향을 주지 않는 항을 의미한다. 보통 ‘X’ 또는 ‘d’로 표기되며, 간략화 과정에서 유리하게 활용할 수 있다.
- 예: 진리표 상에서 특정 입력 조합이 시스템에 존재하지 않거나 결과가 중요하지 않은 경우 → 무관항 처리 가능

2.3 카르노 맵 작성 및 간략화 과정
- 진리표를 기반으로 함수의 SOP 표현을 작성한다.
- 출력이 1인 최소항(minterm)에 대해 카르노 맵에 1을 표시한다.
- 무관항(don’t care)가 있다면 해당 셀에 d 또는 X를 표기한다.
- 인접한 셀끼리 2ⁿ 개씩 묶음(예: 1, 2, 4, 8개 단위)
- 이때 중복 그룹핑이 가능하다.
- 묶인 그룹에서 값이 변하는 변수는 제거하고, 값이 일정한 변수만 유지하여 간략화된 항을 도출한다.
- 묶음 결과를 바탕으로 최종적으로 간략화된 표준형 논리식을 도출한다.



3. NAND 게이트 및 NOR 게이트를 이용한 논리식 변환
3.1 부울 함수의 NAND/NOR 구현 개요
NAND 게이트와 NOR 게이트는 기본 논리 게이트를 대체하여 전체 회로를 구성할 수 있는 범용 게이트(Universal Gate)이다.
- 드 모르간의 정리(De Morgan’s Theorem)를 이용하여 부울 함수를 변형하면 NAND 또는 NOR 게이트만으로 회로를 구현할 수 있다.
- 예: F = AB → F = (A̅ + B̅)̅ → NOR 형태
- 예: F = A + B → F = (A·B)̅̅̅ → NAND 형태

3.2 게이트별 구현 방식
NAND Gate로의 변환
- SOP(Sum of Product)형 논리식은 NAND 게이트로 쉽게 구현할 수 있다.
- AND → NAND → NAND로 연속 적용하면 기본 AND-OR 회로를 대체 가능
NOR Gate로의 변환
- POS(Product of Sum)형 논리식은 NOR 게이트로 쉽게 구현된다.
- OR → NOR → NOR로 변형하여 AND-OR 구조를 대체 가능
예시
- 논리식: F = A·B + C
- NAND 구조:
- A NAND B → A·B 결과 얻기
- 그 결과와 C를 각각 NAND
- 전체를 다시 NAND
- NAND 구조:
- 논리식: F = (A + B)·C
- NOR 구조:
- A NOR B → A + B 결과 얻기
- 그 결과와 C를 각각 NOR
- 전체를 다시 NOR
- NOR 구조:
결론
부울 함수의 간략화는 디지털 회로의 최적화를 위한 핵심적인 기술이다. 부울 대수의 법칙, 카르노 맵, 무관항 처리, NAND/NOR 변환 등의 기법은 논리 회로의 단순화는 물론, 회로 비용 절감과 성능 향상에도 직결된다. 특히, 소형 회로나 임베디드 시스템 등 제한된 자원 내에서 논리를 구현해야 하는 경우, 이들 간략화 기법은 매우 중요한 도구가 된다.