디지털 시스템의 설계에서 논리 회로는 두 가지로 분류된다. 하나는 조합 논리 회로(Combinational Logic Circuit)이고, 다른 하나는 순차 논리 회로(Sequential Logic Circuit)이다. 본 글에서는 조합 논리 회로의 개념과 설계 방법, 그리고 주요 연산 회로들에 대해 정리한다.
1. 조합 논리 회로의 개요
1.1 디지털 시스템의 분류
디지털 시스템은 크게 조합 논리 회로와 순차 논리 회로로 나눌 수 있다.
- 조합 논리 회로는 입력의 조합에 따라 즉각적으로 출력이 결정되며, 과거의 상태는 영향을 미치지 않는다.
- 순차 논리 회로는 현재 입력뿐만 아니라 이전의 상태(과거 정보)에 따라서 출력이 결정되므로, 메모리 기능이 필요하다.

1.2 조합 논리 회로와 순차 논리 회로 비교
| 항목 | 조합 논리 회로 | 순차 논리 회로 |
| 상태 기억 | 없음 | 있음 (메모리 소자 필요) |
| 출력 결정 요소 | 현재 입력만 | 현재 입력 + 이전 상태 |
| 회로 구성 | 논리 게이트만 | 논리 게이트 + 플립플롭 등 기억소자 |
| 설계 난이도 | 비교적 단순 | 상대적으로 복잡 |
- 조합 논리 회로 예시: 가산기, 감산기, 디코더, 인코더 등
- 순차 논리 회로 예시: 레지스터, 카운터, 메모리, 상태기계 등


2. 조합 논리 회로의 분석과 설계
2.1 설계 순서
- 입출력 변수 정의
시스템의 기능에 필요한 입력 변수와 출력 변수를 정하고, 각 변수에 기호를 부여한다. - 진리표 작성
입력 조합에 따른 출력을 나타내는 진리표를 작성한다. - 논리식 도출 및 간략화
진리표로부터 논리식을 도출하고, 카르노 맵(Karnaugh Map)이나 부울 대수를 이용하여 간략화한다. - 논리 회로 구성
간략화된 논리식을 바탕으로 실제 회로를 그린다.
2.2 설계 예시
예시: 3개의 스위치 A, B, C 중 2개 이상이 ON일 때 출력이 ON이 되는 회로를 설계
- 입력: A, B, C / 출력: F
- 진리표 작성
- 출력이 1인 경우의 최소항 도출
- 논리식 도출 후 간략화
- 회로 구성




3. 조합 논리 회로의 종류 – 기본 연산 회로
3.1 가산기 (Adder)
가산기는 두 개 이상의 이진수를 덧셈하기 위한 회로이다. 대표적으로 반가산기(Half Adder)와 전가산기(Full Adder)가 있다.
- 반가산기(Half Adder)
두 비트를 입력 받아 합(Sum)과 자리 올림(Carry)을 출력함- 입력: A, B
- 출력: S = A ⊕ B, C = A ⋅ B

반 가산기 
반 가산기 2
- 전가산기(Full Adder)
A, B 외에도 이전 자리의 자리 올림(Cin)을 입력 받아 세 비트를 더함- 입력: A, B, Cin
- 출력: Sum, Carry-out(Cout)
- S = A ⊕ B ⊕ Cin
- Cout = (A ⋅ B) + (Cin ⋅ (A ⊕ B))
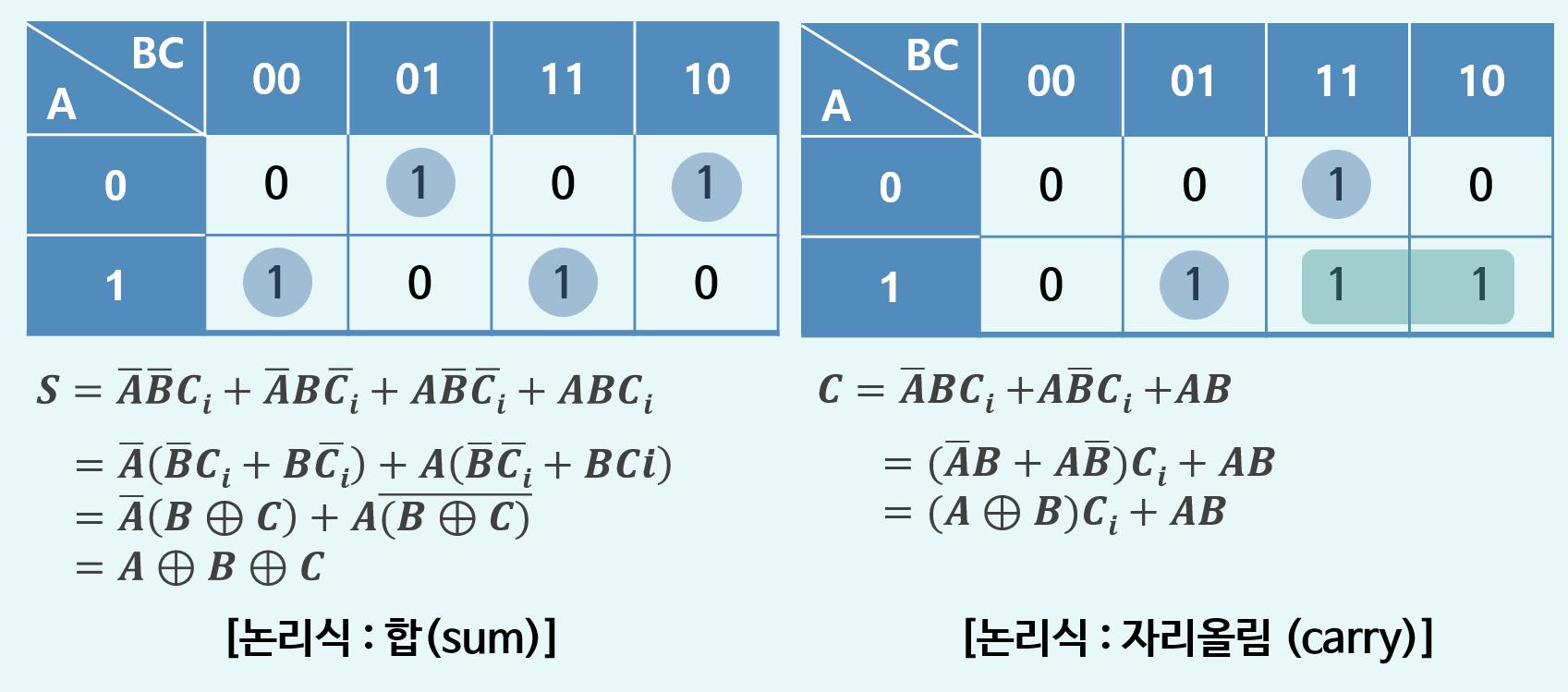
전 가산기 
전 가산기 2 
전 가산기 3
3.2 감산기 (Subtractor)
감산기는 두 비트 간의 뺄셈을 수행하는 회로이다.
- 반감산기(Half Subtractor): 두 비트의 차와 차용(Borrow)을 출력
- 전감산기(Full Subtractor): 이전 자리의 차용까지 고려
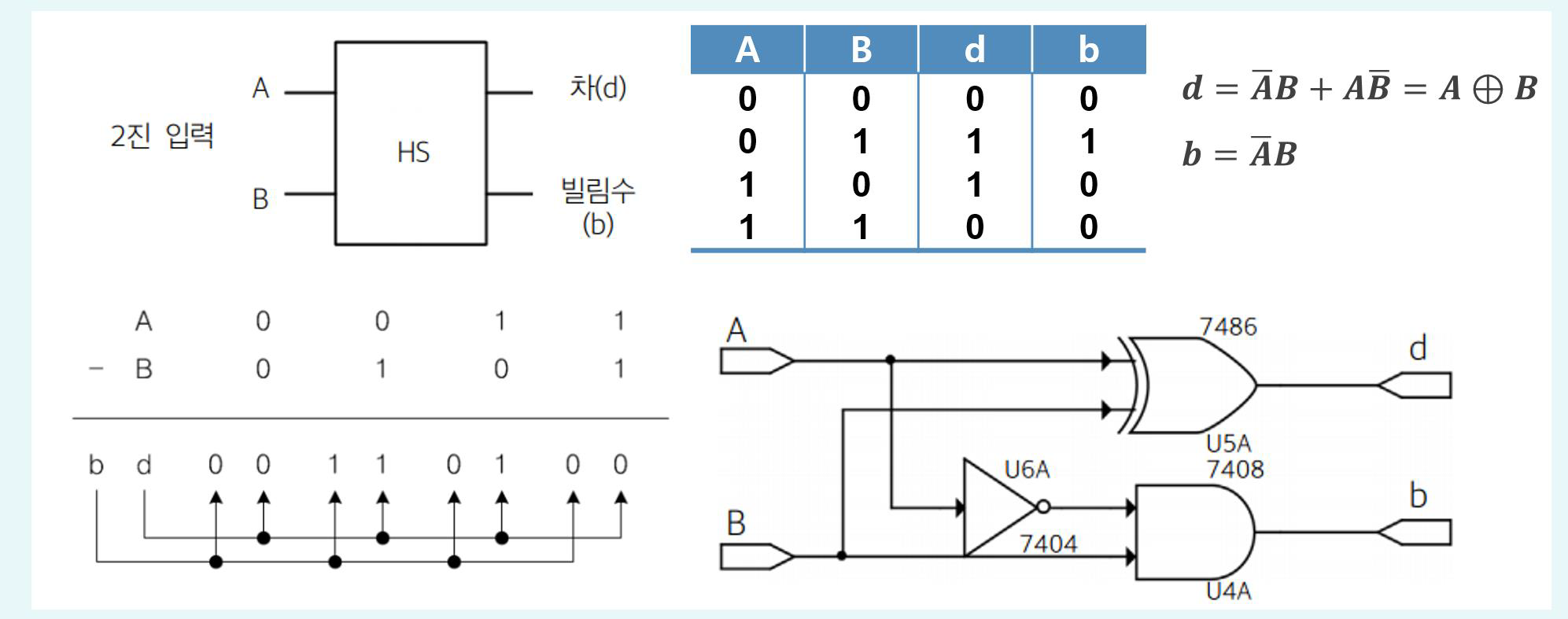
반감산기 
전감산기 
전감산기 2
3.3 병렬 가감산기
- 직렬 가산기: 각 비트를 순차적으로 계산 (속도 느림, 구조 단순)
- 병렬 가산기: 모든 비트를 동시에 계산 (속도 빠름, 구조 복잡)
→ 일반적으로 전가산기를 다수 연결한 Ripple-Carry Adder 사용

3.4 고속 가산기
병렬 가산기는 속도는 빠르지만 캐리 전파 지연(Ripple Delay)이 문제가 된다. 이를 해결하기 위해 캐리 예측 가산기(Carry Lookahead Adder)가 사용된다.
- 원리: 각 비트의 캐리 발생 가능성을 미리 계산하여 전파 시간을 단축
- 장점: 연산 속도 향상
- 단점: 비트 수가 많아질수록 회로가 복잡해짐
→ 계층적 구조(Hierarchical CLA)를 도입하여 해결


4. 결론
조합 논리 회로는 디지털 회로 설계의 기초로, 입력의 조합만으로 출력을 결정한다는 점에서 순차 논리 회로와 구분된다. 특히, 가산기와 감산기 같은 기본 연산 회로는 보다 복잡한 연산 장치의 기반이 되므로 그 구조와 동작 원리를 이해하는 것이 중요하다. 나아가 고속 연산 회로에 대한 이해는 컴퓨터 시스템의 성능 향상과도 직접적으로 연결된다.



